Ask Ethan: Why doesn’t radiation dominate the Universe?

At the start of the hot Big Bang, the Universe was rapidly expanding and filled with high-energy, very densely packed, ultra-relativistic quanta. An early stage of radiation domination gave way to several later stages where radiation was sub-dominant, but never went away completely

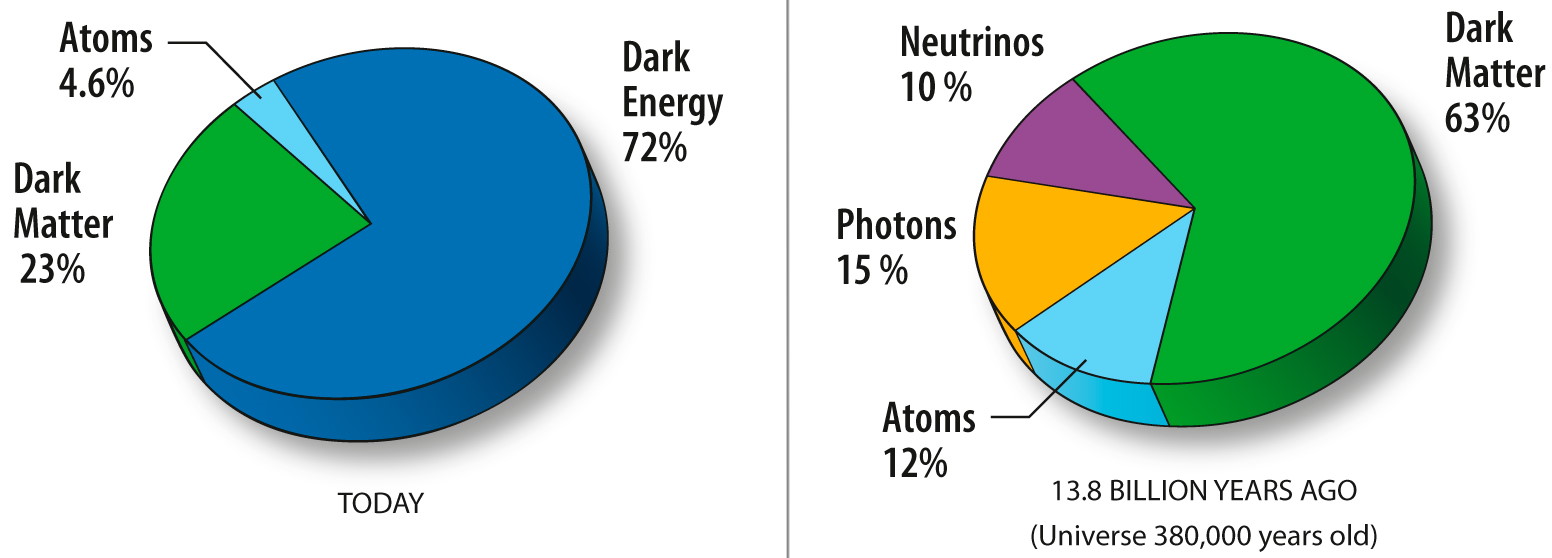
Today, our Universe is filled with stars and galaxies, and is not only expanding, but the Universe’s expansion is accelerating. If we were to break up the Universe into the different types of energy that compose it, we’d find that it was dominated by dark energy, which makes up 68% of the Universe’s energy density. Next would be dark matter, as it composes some 27% of the Universe’s energy density, followed by normal matter (protons, neutrons, and electrons), that makes up about 4.9% of all that’s out there. The other 0.1%? That’s made of things like neutrinos and photons, where all photons and the fastest-moving neutrinos both behave as forms of radiation.

But if you think about how all that radiation came to exist, an enormous amount of it is left over from the Big Bang, and was generated when massive particle-antiparticle pairs annihilated. So why, if there were so many more particle-antiparticle pairs that annihilated as compared with the matter particles that get “left over” as normal matter, doesn’t radiation play a bigger role in the Universe? That’s what Terry Bollinger wants to know, writing in to ask:

“Since the early hot universe was an almost equal mix of matter and antimatter, shouldn’t the total gravitational mass of the cosmic microwave and neutrino backgrounds be billions of times greater than that of fermionic matter?”

The quick answer – before we unpack the in-depth explanation behind it – is that it was greater, once. But no longer. Here’s the science behind why.

Just as raisins within a leavening ball of dough will appear to recede from one another as the dough expands, so too will galaxies within the Universe expand away from one another as the fabric of space itself expands. The fact that all methods of measuring the expanding Universe don’t give the same rate of expansion is troublesome, and may point to a problem with how we presently model the expansion of the Universe.

What you see, above, is an illustration of the expanding Universe. It’s also an illustration of an unleavened ball of dough with raisins randomly sprinkled throughout it. If you were to take this ball of unleavened dough up to the International Space Station – where it would experience effective weightlessness – and let it leaven with time, you’d unsurprisingly find that the dough would expand: roughly equally in all three dimensions. The raisins, meanwhile, won’t themselves expand, but will rather remain embedded in the dough exactly where they were located initially, while the dough between the raisins expands between them.

That’s what the expanding Universe is like: where the “dough” represents the fabric of space and the “raisins” represent individual, gravitationally bound cosmic structures, things like stars, galaxies, groups of galaxies, and even massive clusters or groups of clusters of galaxies. The individual structures, like raisins, don’t expand, but the space that separates the various bound structures from one another, like the leavening dough, does expand. Over time, this causes the Universe to become sparser, less densely populated, and more dilute as the expansion relentlessly continues.

When light is emitted from a source, it has a particular wavelength. The longer it must travel through the expanding Universe before being absorbed by an observer, the greater the amount that the wavelength of that light will be redshifted, or stretched to longer values, compared to the wavelength it has when it was emitted.

That only works, however, because galaxies, like raisins, are governed by a different set of dynamics (being held together in a specific configuration by the gravitational or electromagnetic force, respectively) than the dynamics that govern either radiation or dark energy. Above, you can see what happens within the expanding Universe as:

• one galaxy emits light,
• toward another galaxy,
• and then travels toward it through the fabric of space,
• which is also expanding,
• and whose expansion also stretches the wavelength of the radiation that travels through it,
• until the light finally arrives at the destination galaxy.

Remember that light’s energy, E, is defined by its wavelength, λ, and the constants c (the speed of light) and h (Planck’s constant), via the formula, E = hc / λ. As the Universe expands, say, by a factor of 2, then the wavelength gets stretched to be twice as long as it was previously, which causes the energy of that particular quantum of radiation to then be halved. (As double the wavelength, for radiation, renders it having only half the energy.) Whereas the matter (raisins/galaxies) doesn’t itself change as the Universe expands, the properties of the radiation itself, including its wavelength and energy, do change and evolve.

While matter (both normal and dark) and radiation become less dense as the Universe expands owing to its increasing volume, dark energy, and also the field energy during inflation, is a form of energy inherent to space itself. As new space gets created in the expanding Universe, the dark energy density remains constant.

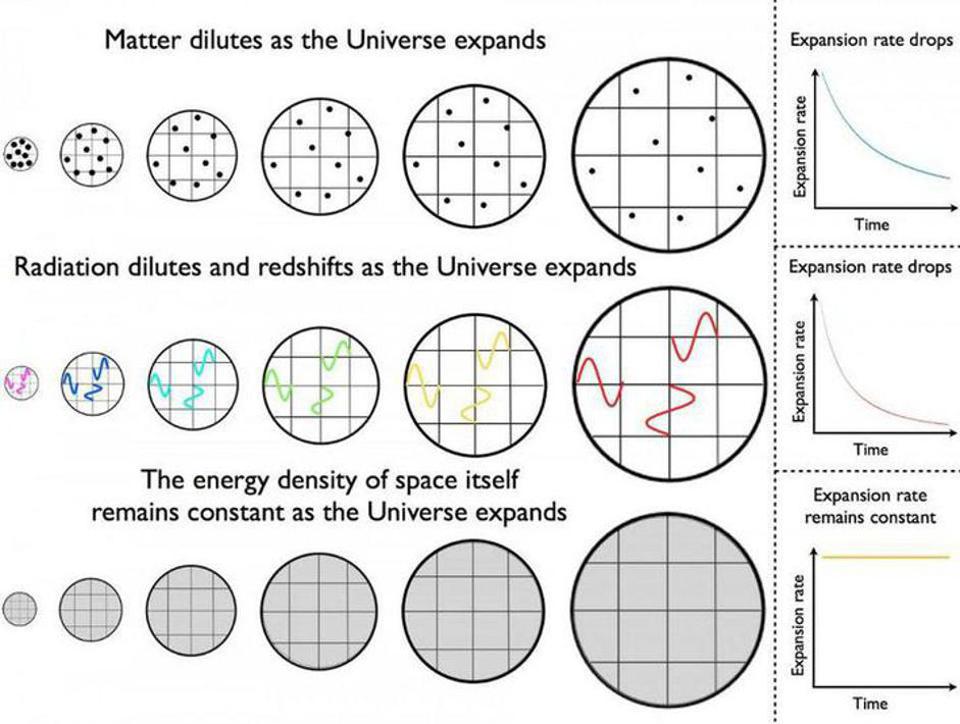
There’s a third type of important energy in the Universe that’s neither matter nor radiation of any class: dark energy. Matter particles themselves don’t change as the Universe expands, but the overall density of matter decreases, as the same number of particles occupies larger and larger cosmic volumes as time goes on. Quanta of radiation do change as the Universe expands, in the sense that their wavelength stretches and their individual energy drops, but they also drop in number density just as matter’s number density drops, causing the energy in radiation to fall off even faster than matter’s energy density with continued expansion.

But dark energy doesn’t do any of that, because it doesn’t behave as either matter or radiation. Instead, it behaves as space: simply creating more and more of itself in between the various quanta of matter (and antimatter) and radiation that exist within the expanding Universe. Because space is just space, its energy density doesn’t drop as the Universe expands, but rather remains constant and doesn’t dilute. This is why, at late times, dark energy comes to dominate the energy budget of the Universe, whereas at earlier times (more than about 6 billion years ago), matter was the dominant form of energy.

Various components of and contributors to the Universe’s energy density, and when they might dominate. Note that radiation is dominant over matter for roughly the first 9,000 years, then matter dominates, and finally, a cosmological constant emerges. (The others do not exist in appreciable amounts.) However, dark energy may not be a cosmological constant, exactly.

But if we extrapolate these trends even farther back in cosmic time than that, look at what occurs according to the graph above. Yes, at very late times, dark energy becomes the only important component to the Universe, as not only do the components that exist (radiation, neutrinos, dark matter, normal matter) continually fall off in density as time goes on, but even theoretical components that might have existed but don’t appear to be present in our Universe (cosmic strings, domain walls, cosmic curvature) would continue to drop off as well. The density of all the other components drops, but dark energy’s density remains unchanged.

But as we go earlier, the matter in the Universe – including normal matter and dark matter (and, at late times/low speeds, neutrinos) – was denser and more closely packed, and that means its energy density was higher and greater in the past. The radiation density, however, rises even more rapidly at early times than the matter density does, as radiation doesn’t just get more closely packed in the early, small-volume Universe, but each individual quantum possesses:

• a shorter wavelength,
• a higher frequency,
• and a greater amount of energy,

the smaller and smaller we extrapolate the size of our Universe to have been early on.

A plot of the apparent expansion rate (y-axis) vs. distance (x-axis) is consistent with a Universe that expanded faster in the past, but where distant galaxies are accelerating in their recession today. This is a modern version of, extending thousands of times farther than, Hubble’s original work. Note the fact that the points do not form a straight line, indicating the expansion rate’s change over time. The fact that the Universe follows the curve it does is indicative of the presence, and late-time dominance, of dark energy.

Whereas today, the Universe is mostly dark energy, it still has a significant but sub-dominant amount of normal matter and dark matter, and only has a tiny amount of neutrinos and photon radiation, this was not the case early on. Back when the Universe was first forming neutral atoms – when the cosmic microwave background was released at an age of just 380,000 years after the hot Big Bang – the Universe was very different: mostly dark matter with some normal matter, but also where photons and neutrinos were important at around the ~10% level as well.

We don’t have mere “snapshots” that provide us with data, either. One thing that’s wonderful about the expanding Universe is that the thing that determines what the expansion rate is, at any moment in time, is the total, overall energy density – across all forms of energy – present in the Universe at that instant. By measuring the redshift-distance relation across our cosmic history, we can determine very accurately what must be the contents of our Universe smoothly throughout time. The same measurements that reveal the presence of dark energy also reveal the energy contents of our Universe, both now and at all moments in our cosmic past.

The matter and energy content in the Universe at the present time (left) and at earlier times (right). Note how dark matter and dark energy dominate today, but that normal matter is still around. At early times, normal matter and dark matter were still important, but dark energy was negligible, while photons and neutrinos were also quite important. The expansion rate is determined by the actual, instantaneous value for density, not by the distribution of the pie chart.

That’s super important! Once we know what the Universe is made out of, precisely, at any moment in time, as well as what the expansion rate was at any moment in time as well, we can immediately figure out what the relative energy densities of every component of the Universe were at any given moment in cosmic time.

The easiest way to do this, both mathematically as well as from an astrophysics perspective, is to make our best measurements of both what’s in the Universe and how fast it’s expanding today, at the present time, and then to extrapolate backward. If we do this, we find that our Universe today is roughly:

• expanding at around 70 km/s/Mpc (with a little bit of tension),
• made 68% of dark energy,
• 27% of dark matter,
• 4.9% of normal matter,
• 0.1% of neutrinos,
• 0.01% of photons,

and a negligible, possibly even 0 amount of other forms of energy (including curvature, cosmic strings, domain walls, and so on). Matter became more important earlier on, from when the Universe was around 10,000 to ~7.8 billion years of age, and then at the earliest times, radiation – mostly in the form of photons but also with a substantial neutrino contribution – was dominant.

The relative importance of different energy components in the Universe at various times in the past. Note that when dark energy reaches a number near 100% in the future, the energy density of the Universe (and, therefore, the expansion rate) will remain constant arbitrarily far ahead in time. Owing to dark energy, distant galaxies are already speeding up in their apparent recession speed from us. Way off the scale of this diagram, to the left, is when the inflationary epoch ended and the hot Big Bang began. Dark energy’s energy density is ~123 orders of magnitude lower than the theoretical expectation.

It might leave you wondering: what happened to all of that energy that was once present in the form of radiation? There are a few different ways of looking at it, all of which are correct in some sense.

• You can claim that the radiation exerts a pressure on the imaginary line that defines the boundary of the observable Universe, and it loses energy in correspondence with the work-energy theorem as it does work in causing the Universe to expand.
• You can claim that the expansion of the Universe is adiabatic – which guarantees constant entropy, but not energy, temperature, pressure, or volume – and so the loss of energy comes about as a consequence of the nature of cosmic expansion.
• Or, you can simply and correctly assert that energy is not conserved in an expanding Universe. In physics, in order to have what’s known as a conserved quantity (something that can be transferred or converted from one form to another, but cannot be created or destroyed), there needs to be an associated symmetry from which that conserved quantity can be derived. The symmetry that corresponds to conservation of energy is time-translation invariance, which means things are the same at all moments in time, and the expanding Universe breaks time-translation invariance, and hence, energy is not conserved.

This simplified animation shows how light redshifts and how distances between unbound objects change over time in the expanding Universe. Note that the objects start off closer than the amount of time it takes light to travel between them, the light redshifts due to the expansion of space, and the two galaxies wind up much farther apart than the light-travel path taken by the photon exchanged between them. The expanding Universe is not time-translation invariant.

But let’s work through how energy was distributed in the early Universe to try and make sense of things explicitly. At the earliest times, there was only radiation: before the electroweak symmetry broke, particles did not yet have rest mass, and so the Universe was ~100% radiation. After the Higgs symmetry breaks, many particles and antiparticles gain positive, non-zero rest masses, and they begin behaving as matter as soon as their kinetic energy (the energy of their motion) drops below their rest-mass energy.

It’s true that, back when the Universe was in its first few seconds, matter and antimatter were both copious at various moments, but always annihilated away to lighter particles and pure radiation. By the time the last antimatter annihilates away (positrons, annihilating with excess electrons), the radiation energy density is billions of times the matter energy density, and around a decillion (~10³³) times the dark energy density.

This diagram shows, to scale, how spacetime evolves/expands in equal time increments if your Universe is dominated by matter, radiation, or the energy inherent to space itself (i.e., during inflation or dark energy dominance), with the latter corresponding to the inflationary phase that preceded and set up the hot Big Bang. Although all of these model universes expand toward infinite size, they approach it at different rates, with the “space itself” solution approaching infinity in a fundamentally more quick fashion than the other two.

And then the Universe expands. Even if you ignore everything else – all the structures that form, all the nuclear reactions that occur, all the stars that live and die, etc. – the expanding Universe will continue to expand, and the relative energy densities of the various species will continue to evolve according to their nature.

• For every multiplicative factor that the Universe expands by, let’s call it a, radiation will have its density drop by a factor of ~1/a⁴, where ~1/a comes from the radiation’s wavelength stretching and where another ~1/a³ comes from the fact that the volume of space expands in three dimensions.
• For matter, its density drops by a factor of ~1/a³, as the 3D volume that space occupies will increase by a factor of a in each dimension, but those are the only changes.
• And for dark energy, its density remains constant, and has no a-dependence at all. (If you insist, its evolution is proportional to a⁰.)

From the time that the Universe was one second old until today, 13.8 billion years later, the Universe has expanded in each dimension by a factor of around 4 billion, meaning that the radiation energy density has dropped by a factor of more than 10³⁸, and the matter energy density has dropped by a factor of nearly 10²⁹. The dark energy density? It hasn’t changed at all.

So yes, the total energy density in radiation was once billions of times greater than the matter energy density, but today, it’s less than 0.1% of the total matter density. Time, evolution, and cosmic expansion, unless you’re dark energy, will eventually dilute absolutely everything else. For radiation, the worst of it has already occurred.
https://bigthink.com/starts-with-a-bang/radiation-dominate-universe/